力扣965题 解题思路和步骤 C++代码实现,力扣题库答案在哪里

题目概述

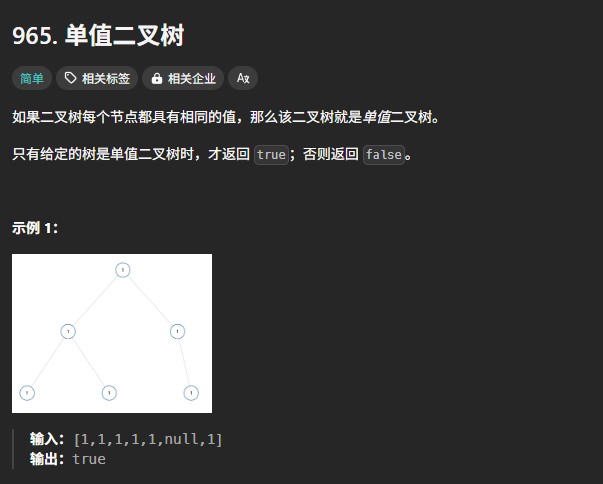
力扣965题是关于单值二叉树的判断。单值二叉树是指二叉树的每个节点的值都相同。给定二叉树 [1,1,1,1,1,null,1]，它就是一个单值二叉树。我们需要编写一个函数来判断给定的二叉树是否为单值二叉树。这就需要对二叉树的结构和节点值进行深入分析。我们要明确解题的大致方向，是通过遍历二叉树的节点来比较其值。那么如何遍历二叉树呢？常见的遍历方式有前序遍历、中序遍历和后序遍历。我们需要选择一种合适的遍历方式来高效地完成判断。在遍历过程中，一旦发现节点值不相同，就可以直接得出该二叉树不是单值二叉树的结论。

对于这道题，我们可以利用递归的方法来实现二叉树的遍历。递归是一种非常适合处理树形结构的算法。通过递归函数，我们可以方便地访问二叉树的每个节点。在遍历过程中，我们还需要考虑一些特殊情况。比如，如果二叉树为空，那么按照定义它也是单值二叉树。所以，在开始遍历之前，我们需要先对二叉树是否为空进行判断。这道题涉及到的关键概念包括二叉树的节点结构、递归算法以及对节点值的比较操作。这些概念的理解和运用对于正确解题至关重要。

解题思路分析

我们可以采用深度优先搜索（DFS）的方法来遍历二叉树。通过递归函数，我们可以从根节点开始，依次访问每个节点。在递归函数中，我们判断当前节点是否为空，如果为空则直接返回true，表示该子树是单值二叉树。我们比较当前节点的值和其左右子节点的值。如果左右子节点的值与当前节点的值都相同，我们继续递归地判断其左右子树是否为单值二叉树。如果在比较过程中发现有任何一个节点的值与当前节点的值不同，或者左右子树的判断结果有一个为false，那么整个二叉树就不是单值二叉树。

对于二叉树 [1,1,1,1,1,null,1]，我们从根节点1开始，发现其左右子节点的值也都是1，继续递归地判断左右子树，最终得出整个二叉树是单值二叉树的结论。在这个过程中，我们需要注意一些边界条件。比如，如果二叉树只有一个节点，那么它必然是单值二叉树。我们可以在递归函数中加入这样的判断，提高算法的效率。这种解题思路的核心在于利用递归的特性，逐步深入二叉树的每一个节点，通过比较节点值来判断二叉树是否为单值二叉树。同时，合理处理边界条件可以使算法更加健壮。像二叉树结构、节点值比较、递归调用这些都是解题过程中密切相关的要素，它们共同构成了我们的解题思路。

具体步骤设计

我们定义一个递归函数来判断二叉树是否为单值二叉树。函数的参数为二叉树的根节点指针。在函数内部，我们先判断根节点是否为空，如果为空则返回true。我们获取根节点的值，记为rootVal。接着，我们递归地判断左子树是否为单值二叉树，同时比较左子树的根节点值是否与rootVal相同。如果左子树为空或者左子树的根节点值与rootVal相同且左子树是单值二叉树，我们继续递归地判断右子树。对于右子树，同样地，我们判断右子树是否为空或者右子树的根节点值是否与rootVal相同且右子树是单值二叉树。如果在整个判断过程中，有任何一个条件不满足，我们就返回false，表示该二叉树不是单值二叉树。在递归调用判断左子树时，如果左子树的根节点值不等于rootVal，我们就不需要再继续判断右子树了，直接返回false即可。

通过这样逐步的判断和递归调用，我们可以准确地判断出给定的二叉树是否为单值二叉树。这一系列步骤的执行顺序和逻辑关系对于得出正确结果非常关键。每一步都紧密相连，共同构建了一个完整的判断流程。

C++代码实现

struct TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

bool isUnivalTree(TreeNode root) {
    if (!root) {
        return true;
    }
    int rootVal = root->val;
    if (root->left) {
        if (root->left->val != rootVal ||!isUnivalTree(root->left)) {
            return false;
        }
    }
    if (root->right) {
        if (root->right->val != rootVal ||!isUnivalTree(root->right)) {
            return false;
        }
    }
    return true;
}

在这段代码中，我们定义了二叉树的节点结构TreeNode，包含一个整数值val和左右子节点指针left、right。我们实现了isUnivalTree函数，该函数按照前面设计的步骤进行判断。函数判断根节点是否为空，如果为空则返回true。接着获取根节点的值rootVal。分别判断左子树和右子树，如果左子树或右子树存在且节点值与rootVal不同，或者递归判断左子树或右子树不是单值二叉树，就返回false。如果整个判断过程都没有返回false，说明二叉树是单值二叉树，返回true。

代码优化与注意事项

虽然上述代码已经能够解决问题，但我们还可以对其进行一些优化。我们可以将判断左子树和右子树的逻辑合并，减少重复代码。优化后的代码如下：

struct TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

bool isUnivalTree(TreeNode root) {
    if (!root) {
        return true;
    }
    int rootVal = root->val;
    if ((root->left && root->left->val != rootVal) || (root->right && root->right->val != rootVal)) {
        return false;
    }
    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

在这段优化后的代码中，我们通过一个逻辑或表达式来同时判断左子树和右子树的节点值是否与根节点值相同。如果有一个不相同，就返回false。再通过逻辑与表达式递归地判断左子树和右子树是否为单值二叉树。

在使用递归时，我们还需要注意递归深度的问题。如果二叉树非常深，递归可能会导致栈溢出。在实际应用中，如果遇到这种情况，可以考虑将递归转换为迭代的方式来解决。代码中的边界条件判断要仔细，确保不会遗漏任何特殊情况。比如，对于空二叉树的判断一定要放在函数的开头，因为这是一个基础的特殊情况。通过这些优化和注意事项，可以使我们的代码更加高效、健壮，更好地应对各种情况。代码的优化和对注意事项的关注有助于提高程序的性能和稳定性，确保在处理不同的二叉树时都能正确地判断其是否为单值二叉树。

通过对力扣965题解题思路的深入分析、具体步骤的精心设计以及C++代码的准确实现，我们能够有效地判断给定的二叉树是否为单值二叉树。同时，对代码的优化和注意事项的把握也能让我们的程序更加完善。希望本文能帮助读者更好地理解和解决这道算法题。

力扣965题 解题思路和步骤 C++代码实现,力扣题库答案在哪里